关于氧化铈不同缺陷形成熵的第一性原理研究

1. 研究背景

众所周知，氧化铈是一种具有萤石结构，带隙约为6 eV的绝缘体。纯氧化铈和异价掺杂氧化铈由于其广泛应用而引起人们关注。它们可应用到涂层材料、研磨材料中，同时也是汽车尾气净化用的三效催化剂的重要组成成分。尽管目前有一些理论计算的工作研究了氧化铈含氧空穴的形成熵，但仍缺乏对氧化铈含其它类型空穴体系的研究。在本案例中，作者系统地研究了氧化铈不同缺陷体系的形成熵，并计算了其体模量、吉布斯自由能等热力学性质。

2. 建模与计算方法

本案例中，作者通过Welcome to MedeA Bundle中的InfoMaticA搜索了具有萤石结构的CeO2，然后采用Supercell Builder创建了2x2x2的超晶胞。根据缺陷的种类不同，分别创建了不同类型单缺陷和掺杂的CeO2结构（O空穴，Ce空穴，O间隙掺杂，Ce间隙掺杂），命名为 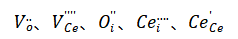   。接着，作者采用MedeA-VASP模块中GGA+U的方法（U值为5 eV），对不同体系进行结构优化。对于优化好的结构，采用MedeA-MT模块计算CeO2结构的振动熵、自由能及体模量等热力学性质。采用MedeA-Phonon模块研究了CeO2不同体系的声子色散曲线和与振动相关的热力学参数。

3. 结果与讨论

3.1 纯氧化铈的体相性质

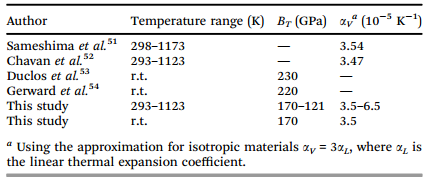
作者采用MedeA-VASP模块对不同体系进行结构优化。随后，作者采用MedeA-MT模块计算了不同体积CeO2结构的体模量、热膨胀系数及其导数。表1文献中实验测试测得的体模量和热膨胀系数。室温下计算值低于实验值，热膨胀系数是给定温度范围内的平均值。

表1   文献中实验测得的体模量和热膨胀系数

3.2 单个点缺陷的形成熵

作者采用MedeA-Phonon模块计算了含有不同缺陷CeO2结构的声子色散曲线；图1给出了含有一个Ce空穴结构的声子色散曲线，经过MedeA-Phonon模块计算，发现没有虚频。作者对其他结构也进行了声子计算，结果都一样，没有虚频，结构稳定。

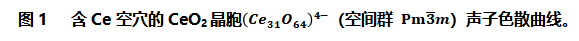
随后，作者计算了两种点缺陷结构的振动熵（见图2左）。恒容室温下，两者的熵值均为定值2.5 kB。对于含单个O空穴的CeO2结构，6个O离子朝空穴移动0.21 Å，4个Ce离子朝远离空穴的方向移动0.16 Å，由此造成含单个O空穴的CeO2体积弛豫是负的，因此在恒压下含单个O空穴的CeO2的熵为负值。相反，含有Ce空穴的结构有较大的体积弛豫，8个O离子朝远离空穴的方向移动0.24 Å，12个Ce离子朝空穴移动0.06 Å，因此在恒压P=0，T=1000 K时，此体系的熵值约为28 kB。

图2右为O间隙和Ce间隙掺杂结构的振动熵。恒容下，两者的熵值也均为定值，Ce间隙会提高晶胞的振动频率，降低晶胞的熵值，因此Ce间隙掺杂结构的振动熵是负值。而O间隙掺杂结构体积弛豫较小，振动熵为正值，与之前实验值一致。恒压下，体积弛豫影响了熵值的变化，O间隙掺杂比之前Ce缺陷的振动熵略小是因为结构弛豫略小。

3.3 Schottky，Frenkel和anti-Frenkel形成熵

由3.2中计算的到的单个缺陷和掺杂的熵值，可以获得Frenkel、anti-Frenkel、Schottky三种实验中缺陷类型的形成熵。计算公式Frenkel（1a）、anti-Frenkel（1b）及Schottky（1c）：

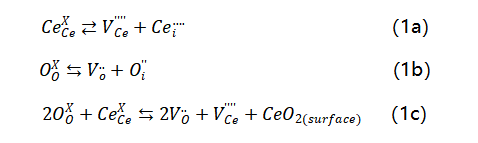
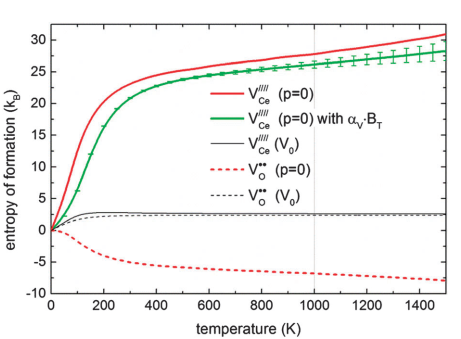
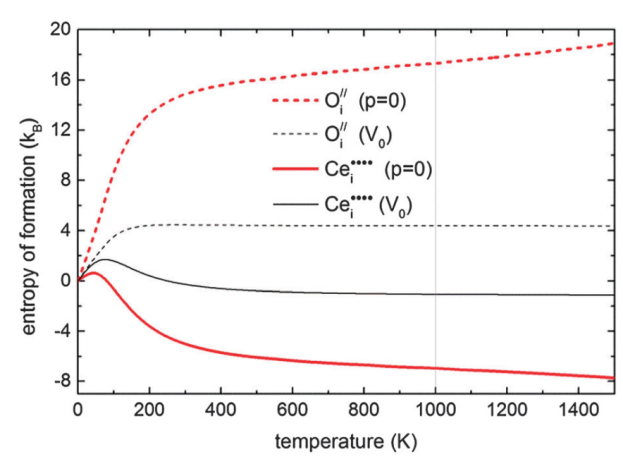
图3给出了CeO2不同缺陷类型的熵与温度之间的关系。图中可以看出在恒压P=0时Frenkel结构的熵最大。形成Ce空穴时会导致晶格参数扩张，而形成Ce间隙则会造成很小的压缩，这些最终会导致CeO2有较大的体积弛豫，使得Frenkel结构的熵较大，如1000 K，Frenkel结构的熵为10 kB。

图3   对于于Frenkel（实线）、anti-Frenkel（虚线）及Schottky（点）结构的熵。熵在恒容V0（黑色细线）及恒压P=0（红色粗线）条件下的数值

3.4 Gibbs自由能

图4给出了恒压P=0不同缺陷结构的吉布斯自由能。在1000K，熵约贡献14%到22%的电子能给吉布斯自由能。

图4    Frenkel（绿色实线）、anti-Frenkel（红色虚线）及Schottky（黑色点）结构的吉布斯自由能

4. 总结与展望

本案例中，作者通过第一性原理研究了含不同缺陷结构的氧化铈的熵，加深了对氧化铈材料的认识，尤其是对氧化铈热力学性质做了非常重要的补充。本案例的研究具有非常重要的科学意义，为日后研究氧化铈熵的改变对缺陷浓度的影响打下了坚实的基础。

参考文献：

Steffen Grieshammer, Tobias Zacherle and Manfred Martin. Entropies of defect formation in ceria from first principles, Phys. Chem. Chem. Phys, 2013, 15, 15935-15942

使用MedeA模块:  

Welcome to MedeA Bundle

MedeA-VASP

MedeA-Mechanical Thermal

l MedeA -Phonon