次临界混合物竞争吸附的理论模型研究

1. 研究背景

吸附现象是分子筛、金属有机框架、纳米多孔材料等工业和学术领域中非常热点的话题。在大部分的实际应用中，研究人员不仅关注单相物质的吸附，更关注多相混合物的吸附。然而，混合相的吸附就会涉及到不同类型分子之间的竞争吸附与吸附平衡，更是涉及到多孔材料的设计问题。目前来说，已经有大量的工作预测了次临界流体的吸附现象，但是大部分都是在低浓度、低压强下的气体吸附。事实上，在更高的浓度和压力下，流体混合相可以凝聚成相当数量的吸附流体层，当达到毛细凝聚压时，则会表现出气/液的两相转变。在本案例中，作者通过统计力学模型，预测了次临界混合相在高浓度及高压下的吸附性质。

2. 吸附模型理论

在吸附过程中，如果是多相混合物吸附，会出现两种不同的吸附层，取决于吸附剂本身的吸附位点，如图1所示。图1模拟了平面上混合物吸附的情况。假如吸附相被分离为两种不同的吸附层类型，在与固体表面接触的第一层，会出现一层均匀、稳定的单层吸附，图1中的Monolayer，每一处的吸附位点都能吸附一个流体分子。然而，当第一层的吸附层达到饱和以后，再往上的第二层吸附层就不再是均匀、稳定的单层吸附了，而将出现多层吸附现象，图1中的Multilayer，这就不局限于一个吸附位点只吸附一个流体分子了。这样的吸附模型正是Langmuir吸附理论的拓展，或者被称作IAST/BET吸附模型。

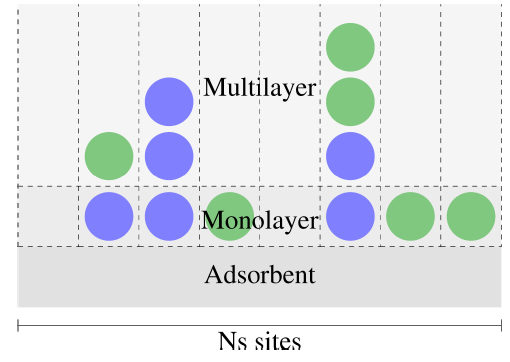
图1 混合相在固体平面的多层吸附草图

在本案例中，作者采用MedeA-Gibbs模块研究了两相合成混合物的Monte Carlo吸附模型。通过MedeA-Gibbs能够模拟出单物质组分以及多物质混合物组分的相平衡状态，从而或得相关的吸附等温线或吸附等压线。本案例中，作者采用的是巨正则系综来进行Monte Carlo模拟，在每个单位的吸附位点上，采用了Lennard-Jones 12-6 势来处理色散力和排斥作用。相关的Lennard-Jones参数见表1。

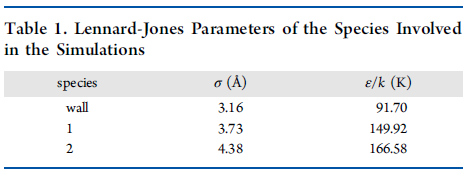
表1 Monte Carlo模拟过程中涉及到的两相多组分的Lennard-Jones参数

固体相模拟的是一类简化的硅酸盐物质，代表了页岩中丰富的无机物组分。大部分固体都是采用巨正则系综来进行Monte Carlo模拟的。组分1的参数对应了甲烷分子，在典型的冷凝气体中，甲烷的成分通常超过60%。流体相由两组分构成，分别对应了组分1和组分2。其物性参数以及热力学条件设为ĸT/ɛ₁= 1 , ɛ ₁/ ɛ₂= 0.9。为了简便起见，选取的组分2的饱和压强大约是组分1饱和压强的三分之一。这也就意味着两种纯物质具有不同的毛细凝聚压力，其吸附等温线如图2所示。通过引入不同的吸附位点，在吸附层中，两组分的吸附物的“位阻现象”也会不同。虽然在模拟的模型中并不会特别考虑，但是“位阻现象”在实际体系中还是客观存在的。

□

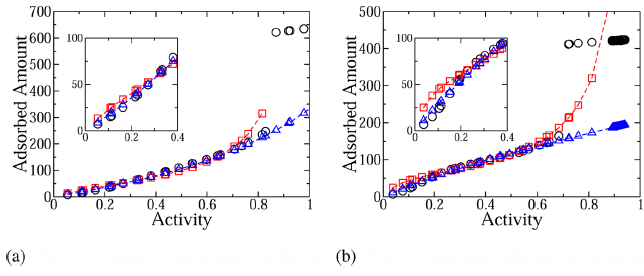
图2 两组分的纯物质吸附等温线。（a）为组分1的吸附等温线。（b）为组分2的吸附等温线。●代表模拟计算结果。□代表与BET模型的拟合结果。△代表与GAB模型的拟合结果。

本案例中研究的孔结构是一类裂孔结构，这类型的孔结构能够轻松识别气体或者液体的吸附机制以及当达到毛细凝聚压力后的不同吸附机制之间的转换。图3表示了这类型孔结构的图解视图。固体相就是FCC晶格，孔径宽度H*定为10×σ₁，固体相一共有6层单相，在长为L_x ，宽为L_z的尺寸内包含了8个元胞。

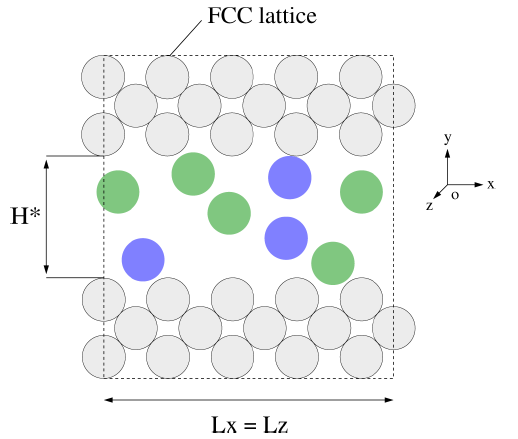
图3 多孔结构用于计算吸附等温线的模拟盒子

    3. 单物质组分吸附

 从图2可知，在实际的吸附过程中，具有两类吸附模型，一类是BET吸附模型，一类是GAB吸附模型。BET是最早提出的多层吸附模型，而在实际情况下，还需要研究多组分的吸附行为，进而提出了GAB吸附模型。表2中列出了混合物两组分相的吸附等温线的计算结果以及均方根偏差。

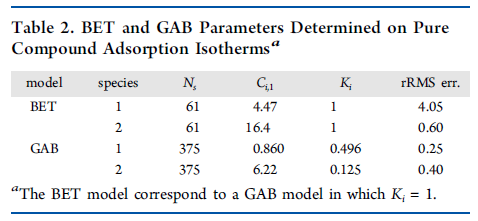
表2 纯物质组分BET以及GAB模型的吸附等温参数

  事实上，不管是BET吸附模式还是GAB吸附模式，都无法避免每一种组分必须占据一整个吸附位点的情况，因此，Ns所表示的组分单层吸附能力对两组分系统来说只能是一样的，这点并不能有效区分开来。因此，采用了某一组分的相关均方根偏差来区分该组分的实际吸附等温线，正如表2所示。

图3分别是两种组分的吸附等温线。由于该两组分不同的Lennard-Jones参数，它们表现出了不同的吸附行为。根据IUPAC的规定，组分1是典型的V型吸附等温模式，由于组分1与吸附剂的亲和作用较弱，在单独的一层吸附层中无法保证吸附物在每个吸附位点都均匀展开，因此多层吸附模式比单层吸附模式更有优势。不同的是，组分2则是典型的IV型吸附等温模式，其溶质吸附物组分与溶剂流体在吸附层表面有很强的亲和作用，因此在单层就很容易铺开，组分2的吸附量会更大。相比之下，V型吸附等温行为较难复制出BET吸附模式，而且V型吸附效率会比VI型更低一些，这也与图3（a）的吸附曲线是凹型的图像相吻合。

    4. 多物质组分吸附

对于多物质组分吸附的研究，重点在与两方面。一方面是区分混合物多组分的成分，另一方面是预测每种吸附组分的吸附量。

     4.1 吸附相组分选择性

为了准确估计吸附相的组分，则需要计算出不同组分的相关吸附选择性。在本案例中，作者研究了三种模式的流体吸附选择性，如图4所示。

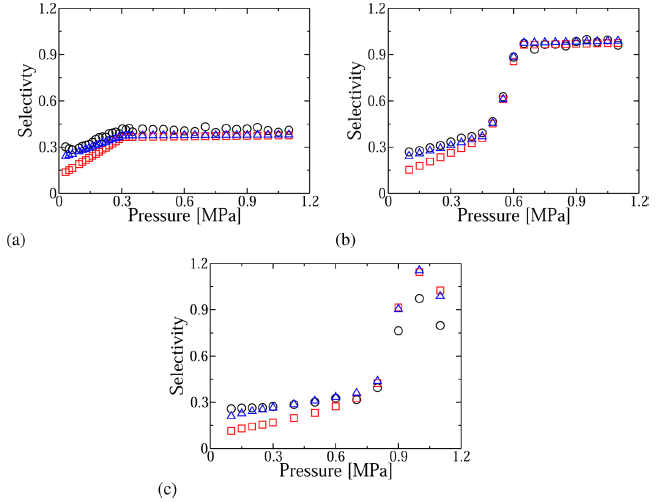
图4 吸附选择性与压强的关系曲线。（a）10%的组分1与90%的组分2的多物质组分系统，（b）50%的组分1与50%的组分2的多物质组分系统，（c）90%的组分1与10%的组分2的多物质组分系统。●代表模拟计算结果。□代表与BET模型的拟合结果。△代表与GAB模型的拟合结果。

图4展示了三种多物质组分系统的吸附选择性与压强的关系。压强的范围从0.1到1.1 MPa，从图4（a）可知，对于10%的组分1与90%的组分2组成的混合系统，选择性并不这么明显，因为对于只有10%组分1的混合体系，其混合物毛细凝聚现象并不那么明显，因此将组分1和组分2进行选择性区分的效果也并不好，这与组分的成分有非常大的关系。相比之下，当两组分是以50%的组分1与50%的组分2构成的系统的时候，选择性曲线随着压强的变化会发生很剧烈的转变。毛细凝聚现象会迫使整个系统从气态向液态转变，如图4（2）所示。从整个相转变的拐点来看，图4（a）是在0.3 MPa压强下，图4（b）是在0.4MPa压强下，图4（c）在0.7 MPa压强下。尽管物质的吸附选择性与压强的关系表现出的是非单调曲线，但是E-GAB吸附模型依然提供了与气态或液态组分相吻合的选择性预测。

     4.2 吸附相组分的吸附量测定

图5展示了两组分的吸附等温线。其吸附量代表了孔结构中吸附的分子数目。

图5 两组分相的吸附量与压强的关系。（a）10%的组分1与90%的组分2的多物质组分系统，（b）50%的组分1与50%的组分2的多物质组分系统，（c）90%的组分1与10%的组分2的多物质组分系统，（d）组分1与含90%的组分2混合后，再与10%的组分2混合的混合系统。●代表模拟计算结果。□代表与BET模型的拟合结果。△代表与GAB模型的拟合结果。

对于在毛细凝聚点以上的环境下，BET或者是GAB吸附模型都不能很好的预测组分的吸附量。尤其是在混合体系中存在某种组分含量比较大的情况。比如在图5（c）（d）中，BET模型的吸附量明显会高于实际值。然而，其选择性的预测还是十分准确的，如图4（c）所示。虽然各个组分的毛细凝聚值不同，但是多组分毛细凝聚的交叉点并没有影响到组分间相互作用参数的变化，因此其余贡献到吸附计算中的各组分参数依然能够改进毛细凝聚点的吸附模型，并准确计算出单层吸附量Ns的值。

     5. 总结与展望

在本案例中，作者通过MedeA-Gibbs模块预测了混合物双组份的吸附性质，通过对吸附组分的分析以及吸附量的计算，完善了从低压到高压环境下混合物双组份的吸附等温线的数据结果。MedeA-Gibbs计算的结果与Langmuir、BET、GAB等著名的经典吸附模型也具有很好的吻合性。虽然理论模型与实际情况依然有一定的偏差，但是随着理论的发展以及数据量的不断完善，双组份甚至是多重组分的吸附性质都将获得越来越准确的结果。在实际生产、生活中，很多领域都涉及到了物质吸附性能的研究，比如食品工程、炼油分离过程、精糖工业等等。MedeA-Gibbs是专门用于计算物质相平衡以及吸附性质的模块，能更好的预测单相或多相的热物理学性质。

    参考文献：

    Julien Collell, Guillaume Galliero. Theoretically Based Model for Competitive Adsorption of Subcritical Mixtures. Journal of Physical Chemistry C. 2014, 118, 26162-26171.

    使用MedeA模块:  

• Welcome to MedeA Bundle

• MedeA-Gibbs